離散型機率分布: Bernoulli Distribution、Binomial Distribution、Poisson Distribution
機率分布大致有兩類：離散型 Discrete Distribution，和連續型 Continuous Distribution。離散型分布是指獨立離散的機率，而連續型分布是指機率是無縫緊連地出現。
例如：
- 離散型分布：P(10) = 0.16
- 連續型分布：P(10-20) = 30
離散型分布，包括：伯努利分布 Bernoulli Distribution、二項分布 Binomial Distribution、卜瓦松分布 Poisson Distribution。
我會在本篇文章簡述離散型的機率分布。
==============================
伯努利分布 Bernoulli Distribution
當結果只有二元，伯努利分布 Bernoulli Distribution 就適合使用，例如：A 或 非 A；成功或失敗；Yes 或 No。
假設：擲硬幣，後果只有 Head, H， 或 非 H （即 Tail, T）。
即：H 出現時的事件，假定為 X = 1； 非 H 出現時的事件，假定為X = 0。
- H 出現的機率，P(H) = p;
- 非 H 出現的機率，P(-H) = 1 - p；
- H 或 非 H 出現的機率的總和 = 1；即：P(H) + P(-H) = p + 1 - p = 1。
把 H 出現的次數設為隨機變數 random variable X ，而 X 的機率質量函數 Probability Function 就是 Eq. (1)：
當 k = 0 是非 Head，k = 1 是 Head。
當 Head 出現，k = 1 ：
當 Tail 出現，k = 0 ：
可見，結果只有二元：
- 當 H 出現，k = 1 ：P(X=1) = p
- 當 非 H 出現，k = 0 ：P(X=0) = 1 - p
如用隨機變數 random variable X 來表示機率分布，就是機率 p 的 Bernoulli Distribution， Be(p)。Figure 1 是 Bernoulli Distribution 的例子，呈現離散分布在二元結果，k = 0 和 k = 1 ，之上。
Be(p) 的平均值是 p，而 variance 是 p (1 - p)。
=================================
二項分布 Binomial Distribution
當結果只有二元的事件機率 p 的 Bernoulli Distribution [P(X=1)= p] 重複執行 n 次時，把 H 出現的次數設為隨機變數 random variable X ， 便附合 Binomial Distribution。下面是的 X 的機率質量函數 Probability Function， in Eq. (2)：
Eq. (2) 也可以寫成 Eq. (3)：
從 Eq. (2) 和 (3) 可見，Binomial Distribution 只有一個 term 跟 Eq. (1) Bernoulli Distribution 不同的，就是 nCk (binomial coefficient)。Binomial Distribution 因為要解釋 Bernoulli Distribution 重複 n 次的可能組合，所以要包含這個 term。
要留意，這裡的 k 因為有重複數據，所以不再跟Bernoulli Distribution的 k 一樣，只有兩個可能組合，並非只有 k = 0 或 k = 1。而是有 nCk 的可能組合！
這個二項分布 Binomial Distribution，稱為 Bin(n, p) 。
- Bin(n, p) 的平均值是 n p，而 variance 是 np (1 - p)。
- 而 Bin(n, p) 與 Be(p) 是一致。
例子 1：
某推銷商推銷生意的成功率為 55%。將其推銷成功次數設定為隨機變數 X。請計算它五次推銷中，三次成功的機率有多少？
答案：
n = 5; p = 0.55; k = 3
其他例子，可以參考 <貝氏定理 (4): Likelihood in Bayes Rule> 內的 Likelihood Estimate using Binomial Distribution。
=====================================
卜瓦松分布 Poisson Distribution
這是一個與罕見事件發生次數相關的機率分布。Poisson distribution 是用來計算，在某限定時間或空間間隔 interval 內，罕見事件發生的次數。
- 這個罕見事件，在某時間內，以往平均發生的次數，便是隨機數： λ。
- λ = n p
- 而要預測它在未來同等時間間隔 interval 內發生這個罕見事件的次數，便是隨機數： k。
附合 Poisson Distribution 的 X 的機率質量函數 Probability Function is in Eq. (4)：
- Po(λ) 代表 Poisson Distribution。
- Po(λ) 內的平均值是 λ； Variance 也是 λ。
從 Binomial probability function equation, Eq. (3), derives the equation for Poisson probability function Eq. (4):
當 n → ∞，
因罕見事件，所以 p → 0：
因為 Bin(n, p) 的平均值是 n p，所以 λ = n p
像 Binomial Distribution 一樣，當 λ 愈大，愈接近 Normal Distribution。
例子 2：
某城市平均每天有四宗交通意外，假設這個城市每天的交通意外為 X，而X 是服從 Poisson Distribution。那麼，明天該城市有三宗交通意外的機率有多少？
答案：
λ = 4; k = 3
可服從 Poisson Distribution 的例子：
- 某作家的錯別字的出現；
- 某城市每天交通意外；
- 某國家每年被黑客入侵數字；
- 某公司每天被電話騷擾次數；
- 急症室每小時被電話騷擾次數；
- 某國家軍隊的陣亡人數。
註：恐襲是極罕見事件，應該屬於肥尾曲線 Fat-tailed Distribution 而非 Poisson Distribution。
Reference
石井俊全，統計學關鍵字典，楓葉社， Unknown year。
=======================
免責聲明
本網頁屬個人網誌，一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性，包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏，而導致之任何損失或損害，本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產，均受知識產權法例及權利（包括但不限於保護版權的法例）所保障。根據此法例及權利，任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下，本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
© Copyright 2021-2022 高山雪 Snow Hill. All rights reserved.
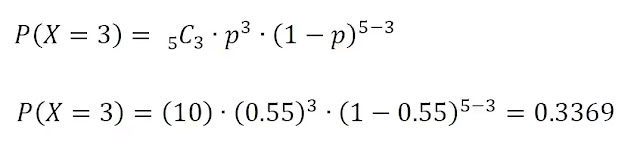
留言
發佈留言