展望理論 Prospect Theory (1): 價值函數 (Value Function)
展望理論 (Prospect Theory) 是由兩位以色列經濟學家,Daniel Kahneman (丹尼爾·康納曼) 和 Amos Tversky (特沃斯基)在 1979 年在 Econometrica 的學術刊物中提出的,文章題為:“Prospect Theory: An Analysis of Decision under Risk” (展望理論 :風險決策的分析)。Daniel Kahneman (康納曼)更因為在此研究領域上的貢獻,獲得 2002 年諾貝爾經濟學獎。要不是Amos Tversky 在 1996 年逝世,他必定與Kahneman分享諾貝爾經濟學獎。他們的研究是關於風險決策理論 -即:展望理論,指:人在自己獲利和損失的情景下,處理風險的態度差異,以致作出不同決定。推翻了以往期望效用理論中,只看效用值來作決定。
本課題會分成六部分文章來解釋展望理論,首四部分是較為學術的基礎理論(但程度不高,屬可普遍博覽的程度),最後兩部分是實際使用:
第一部分:展望理論中的價值函數;
第二部分:展望理論中的機率加權;
第三部分:確定效應;
第四部分:參考點的影響;
第五部分:如何應用在投資上;
第六部分:股市應用 --- 違反人性的風險決策
Photo by Morgan Housel on Unsplash.
展望理論 (Prospect Theory) : 基礎
展望理論是指人類是非理性的,而且有損失規避的自然傾向。在作決策時,不是純粹理性地看期望值或期望效用值的高低,也非只是尋找價值或效用最大化來作決定,而是受到情景影響下的心理因素加權來作決定。那些因素包含了四大展望理論特徵,包括:
- 參考點的依賴:依賴主觀設定的參考點(隨時間、情景、遭遇影響而可以有所變動);
- 敏感度遞減 (Diminishing Sensitivity);
- 損失規避 (Loss Aversion);
- 確定效應 (Certainty Effect);
這些因素會令人對風險處理的態度轉變,而作出一些不理性的決策 (irrational decision making)。
展望理論把期望效用理論中的機率 (pi) 和效用結果 U(∙) 優化成 w(p) is probability weighting function (機率加權函數)和 v(x) is value function (價值函數) 。
展望理論值 (PT value) 的計算公式:
展望理論值 = w(p) × v(x)
where w(p) is probability weighting function (機率加權函數); v(x) is value function (價值函數)
把所有每個發生事件的機率加權函數 w(pi) 和價值函數 v(xi) 的乘積再加總,便可得出 PT value 整體價值模型是:
where w(p) is probability weighting function (機率加權函數); v(x) is value function (價值函數)
- 在本部文章先解釋價值函數計算及意義分析,機率加權函數會留待第二部分文章闡述,而確定效應則會第三部分。
價值函數 (Value Function)
展望理論價值函數 (value function) 可以說是累積展望理論 (Cumulative Prospect Theory) 的核心模型。最原始的模型是:
where v(x) 是價值函數 (value function);而 x 是價值;𝛼 是涵數;𝛌 是因為人們感受損失的的濃烈程度比獲利大 2 至 2.5 倍,這裏取 2.5 倍 。 v(0) 是 0。以上方程式道出,當獲利時 (x ≥ 0),價值函數是:
當損失時 (x < 0),價值函數是:這顯示在損失時的價值函數的數值是 2.5 倍高於獲利時的同等價值。
下圖 (Figure 1) 展現了一個模擬價值涵數圖,用 value function (Y-axis) 與相對賺蝕價值 (X-axis)。在圖中,
- 縱軸向上而 v(∙) 呈正數值,對個人有正的效用值,即開心、快樂、滿足等正面感受。;而縱軸向下,v(∙) 呈負數值,對個人有負的效用值,即損失、失去、痛苦等負面感受價值。
- 橫軸是指實質相對價值,相對於 x = 0,如正數值, x > 0,就視之為獲利,由於是相對於在參考點上的 x = 0, 即 v(0) = 0,所以是「相對獲利」。相反,如負數值, x < 0,就視之為「相對損失」。
Figure 1. Prospect Theory value function 展望理論價值函數,𝛼 = 0.5;𝛌 =2.5。(Nicholas C. Barberis, Thirty Years of Prospect Theory in Economics: A Review and Assessment, Journal of Economic Perspectives, 27, (1), 2013, 173–196)
在 Figure 1 的價值函數圖可以清晰看到:
- 不對稱的 S 型,亦即獲利和損失的價值函數是不對稱。一般,人們感受損失的的震撼程度比獲利大 2 至 2.5 倍。所以在相對損失下的價值函數是比同等獲利的價值函數的變幅為大,故呈現不不對稱的 S 形狀。而這 S 的形狀是因人而異。
- 價值函數是從參考點的移動而得來的數值,並非一個絕對值。而即使是同一個人,設定不同參考點,也會有不同的 S 形狀。這就是參考點依賴 (reference point dependence)。
- 在接近參考點的左右兩旁的正負價值函數變化(斜度)是特別強,即價值小的比價值大的斜度為高,這就是敏感度遞減 (diminishing sensitivity)。
- 價值函數的斜度變化中,負的比正的斜度高。就是說,在損失下的價值函數比同等的獲利價值的價值函數為高,亦即是人們會重視避免損失多於獲利,這就是損失規避 (loss aversion)。
(1) 參考點的依賴
在展望理論中的價值函數 v(x)是一個相對於參考點的相對獲利或損失的函數,並非絕對數值。其重點在於,參考點決定了感受獲利或損失,著重價值的變化,而並非從最終淨財富的多少來決定獲利或損失。所以,價值函數是 v(x),而非如期望效用值的 v(W+x)。即使參考點是設定在 W,價值函數也是 v(x),因為 x 是由價值的變化來計算。
例子 (2): Q 的資產從 3000 萬跌至 2000 萬, 而 R 的資產從 1000 萬升至 1500 萬,誰較快樂?
大多數人會說,R 較快樂,原因是參考點的設定。
Q 的參考點設定在 3000 萬時,價值函數是 v(-1000萬);而 R 的參考點設定在 1000 萬時,價值函數是 v(500萬)。所以人們看到的資料是損失 1000 萬與獲得 500 萬的比較。不要忘記,損失的的震撼程度比獲利大 2 至 2.5 倍,而且人類有種損失趨避的傾向,就是盡可能不想有損失,即是少賺也好,也不想有損失。所以大多數人會認為 R 會較快樂。
但如果用 $0 作為參考點,Q 的價值函數是 v(2000萬);而 R 是 v(1500萬)。結果是 Q 較快樂。現在看到的畫面卻完全不一樣,價值函數也完全不一樣,結論當然也不一樣。結果與之前的剛剛相反。
參考點是可以變動的,可以與金錢、健康、際遇、不同情景的改變而變動參考點。 而參考點的改變是可以影響人的判斷,進而影響風險決策。
在第四部分文章,會有關於參考點設定的更深入探討:
展望理論 (4): 參考點的影響 (Reference Point Influence)
(2) 敏感度遞減
敏感度遞減是說,人們不論是獲利或損失,正負效用,對數值小的變化的敏感度是高於數值大的變化。當數值小時,價值函數 v(x) 的變化特別大,斜度也很大。隨著數值愈來愈大,價值函數的變化會變得愈來愈少,斜度也放平。這現象跟「邊際效用遞減」相似,獲利或損失的「邊際價值遞減」。在正效用時,「邊際價值遞減」的幅度較大,價值函數的斜度較平。但是在負效用時,「邊際價值遞減」的幅度較少,價值函數的斜度較高,這是損失規避。
例子 (3):
A: 25% 可以損失 $6,000 ;
B: 25% 損失 $4,000;25% 損失 $2,000
例子 (4):
C: 25% 可以獲得 $6,000 ;
D: 25% 獲得 $4,000;25% 獲得 $2,000
在例子 (3),大多數人會選 A;在例子 (4),多數人會選 D。原因也是敏感度遞減。
例子 (3): 0.25 v(-6000) > 0.25 v(-4000) + 0.25 v(-2000)
例子 (4): 0.25 v(6000) < 0.25 v(4000) + 0.25 v(2000)
在例子 (3),因為人們看損失 $4,000 或 $2,000 比損失 $6,000 更敏感,即是 0.25 v(-4000) + 0.25 v(-2000) 得出來的負數比 0.25 v(-6000) 的負數更大(更負),所以損失 $4,000 或 $2,000 的價值函數比損失 $6,000 更大。基於人有損失規避的傾向,所以多數人會選 A。
而相反,在例子 (4),人們看獲得 $4,000 或 $2,000 比獲得 $6,000 更敏感,所以多數人會選 D。
敏感度遞減與風險態度
以上兩個例子說明,人們看價值變化時的敏感度,不是以線性地增減,而是隨著價值的增加而減少敏感度。而因為敏感度遞減,人會對風險的態度在損失或獲利時有所差異。
在高機率情景下:
- 在損失時,人會較偏好風險 (Risk seeking);
- 在獲利時,人會較規避風險 (Risk aversion)。
例子 (5):
A: 80% 可以獲得 $8,000 ;
B: 100% 可以獲得 $3,000
例子 (6):
C: 80% 可以損失 $8,000 ;
D: 100% 可以損失 $3,000
在例子 (5),在獲利時,多數人會選 B;在例子 (6),在損失時,多數人會選 C。
雖然選項 A 的效用值比 B 的效用值為大,但是人在獲利時,會較為規避風險,加上 B 的 100% 機率,就是確定效應高估了結果總值的傾向,以致多數人寧願選效用值較少的 B(即:0.8 × 8000 < 1.0 × 3000)。
在損失時,例子 (6),人會較為偏好風險,所以會有較多人選擇金額較大但機率較少的 C,而非金額較少的肯定損失(即:0.8 × -8000 > 1.0 × -3000)。。
可是這個風險態度也跟機率的多少相關,以上的一般觀察,只限於高機率情況。而其他情況則在第二部分文章說明。
(3) 損失規避
在 Figure 1 的價值函數圖,在正效用時,敏感度遞減的幅度較大,價值函數的斜度較平。但是在負效用時,敏感度遞減的幅度較少,價值函數的斜度較高,這是損失規避。也因為損失規避,形成了價值函數圖的正負兩邊的不對稱性很強。也就是說,人們對負面的刺激的敏感度高於正面的刺激。
用實驗數據, 以上的價值函數 (value function)的模型可重塑為:
where 𝛼 涵數是 0.88;𝛌 是 2 至 2.5 倍的中位數 = 2.25。 v(0) 仍然是 0。
例子 (7):
A: 100% 獲利 $100 ;
B: 100% 損失 $100
這說明,同樣大小的金額在獲利和損失時,人們在心裏計算的價值是不一樣的。同樣的 100 元,在人們的心裏,獲利時的價值函數是57.54;但在損失時,卻有多於兩倍的損失感而得出價值函數 -129.47。很明顯,損失對人帶來的痛苦感比獲利時帶來的快樂感為大。所以,人會避免損失而造成損失規避。
人們到底有多害怕損失,那就是依賴他以前的經驗及其身處的現況,這是與參考點設定有關。舉例,某某之前賺了大筆錢,他會比其他沒有賺錢的人和虧錢的人較少程度損失規避。因為參考點設定在未有賺錢之前;但如果他的參考點設定在賺錢之後,那就跟其他人無異。相反,虧錢的人,多數會把參考點設定在虧錢之後,那便令他更加規避損失。對小數值的損失也相當敏感,而得出相對大的負價值函數。
一次性的獲利或損失 vs 兩次的獲利或損失
以上的價值函數 (value function)模型也可以用來解釋,對於同等價值而言,到底一次性的獲利還是分兩次的獲利會較愉快?一次性的損失還是分兩次的損失會較痛苦呢?
例子 (8): 一次性獲利 $200 vs 兩次獲利 $100
例子 (9): 一次性損失 $200 vs 兩次損失 $100
從以上兩個例子可見,對於同等價值 200 元,不論是獲利或損失,分兩次得出的價值函數也高於一次性的價值函數,這代表兩次獲利 $100 的快樂感比一次獲利 $200 為高,而兩次損失 $100 比起一次性損失 $200 更為痛苦。原因是分兩次的獲利或損失,第二次的參考點是基於第一次的得失而移動,而且其移動速度快。
(4) 確定效應
因篇幅所限,機率加權函數會留待第二部分文章,而確定效應則會第三部分文章闡述:
References
Nicholas C. Barberis, Thirty Years of Prospect Theory in Economics: A Review and Assessment, Journal of Economic Perspectives, 27, (1), 2013, 173–196
Nicholas Barberis and Ming Huang, Stocks as Lotteries: The Implications of Probability Weighting for Security Prices, American Economic Review 2008, 98, (5), 2066–2100.
友野典男,有限理性: 行為經濟學入門首選,大牌出版。
=======================
免責聲明
本網頁屬個人網誌,一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性,包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏,而導致之任何損失或損害,本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產,均受知識產權法例及權利(包括但不限於保護版權的法例)所保障。根據此法例及權利,任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下,本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
(c) 2021 高山雪 Snow Hill. All rights reserved.







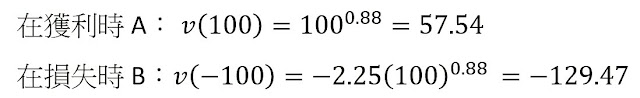
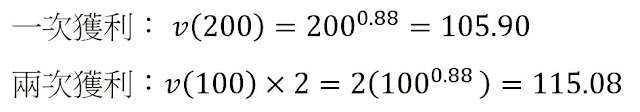










留言
發佈留言