機率思維 | 蒙堤霍爾困境 (Monty Hall Problem)
誤解:很多人會認為,既然 Z 門後沒有獎品,剩下來的 X、Y 門後有獎品的機率是各 1/2。換門沒有增加獲獎機率,於是大多數人也選擇不換門。
答案:這個 1/2 機率似乎合理,但關鍵資訊是:節目主持人是事先知道獎品是放在哪扇門後,即是說:他開的門必然是沒有獎品的哪扇門,他才會可以問你是否選擇換門。
- 一開始,X、Y、Z 門後有獎品的機率是各 1/3。
- 你選擇了 X 門。
============================================
Scenario 1: 你選了 X 門,X 門後有獎品,Z 門打開
Figure 2. Decision tree of choosing Door X if Door X gets a reward. Probability is in parenthesis.
A:你選了 X 門,X 門後有獎品 (X= True),Z 門打開
B:你選了 Y 門,Y 門後沒有獎品 (Y= Wrong),Z 門打開
你選對的機率 = P(X=True | Z open):
⇒ 你選錯的機率 = P(X=Wrong | Z open):
結果:應該是要換門;
因為:
======================================================
Scenario 2: 你選了 X 門,Y 門後有獎品,Z 門打開
假設 Hypothesis B: 你選了 X 門,Y 門後有獎品 (X= Wrong),Z 門打開
A:你選了 X 門,X 門後沒有獎品 (X= Wrong),Z 門打開
B:你選了 Y 門,Y 門後有獎品 (Y= True),Z 門打開
你選錯的機率 = P(X=Wrong | Z open):
B:你選了 X 門,Y 門後有獎品 (Y= True),Z 門打開
⇒ 你選對的機率 = P(X=True | Z open):
結果:應該是要換門。
原因:跟上面一樣
==================================================
友野典男在他的著作<有限理性>提供一個超簡單的解釋:
- X 門後有獎品的機率 = 1/3,
- 那麼,Y 門或 Z 門後有獎品的機率 = 1 - 1/3 = 2/3。
- 現在知道 Z 門後是沒有獎品,即 Y 門後有獎品的機率 = 2/3。
所以,結果是:應該是要換門。
==================================================
改變關鍵訊息:主持人事前不知道
這個「應該要換門」的結論,是基於主持人是事先知道哪扇門後有獎,而有心不開哪扇有獎的門。
假設,那主持人是不知道哪扇門後有獎,而隨意選擇開哪扇門,而他開的門是有機會是有獎的。現在他亦開了 Z 門,那麼,你是否再選擇換門呢?
答案:
你選對的機率 = P(X=True | Z open):
⇒ 你選錯的機率 = P(X=Wrong | Z open) = 1/2結果:沒有必要換門。
因為:換門不能增加你得獎機率
結語
這個 Monty Hall Problem 看似很難懂,實質是大多數人也忽略了一個重要關鍵,就是「那主持人是事先知道哪扇門後有獎,而有心不開哪扇有獎的門」。這個關鍵影響了機率的計算。相反,如果那主持人是事前不知道哪扇有獎的門而隨意開的話,結果是我們的 common sense 的選擇。Monty Hall Problem 的設計是為了設下陷阱讓人墮入。
References
友野典男,有限理性: 行為經濟學入門首選,大牌出版。
石井俊全,統計學關鍵字典,楓葉社, Unknown year。
=======================
免責聲明
本網頁屬個人網誌,一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性,包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏,而導致之任何損失或損害,本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產,均受知識產權法例及權利(包括但不限於保護版權的法例)所保障。根據此法例及權利,任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下,本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
(c) 2021-2022. 高山雪 Snow Hill. All rights reserved.







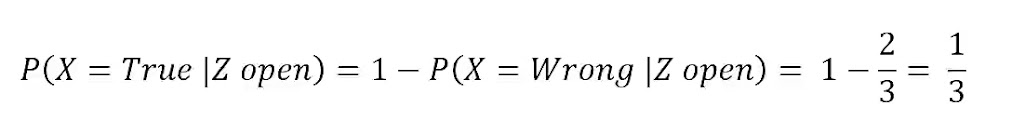












留言
發佈留言