賽局理論 (Game Theory): 囚徒困境 (Prisoner's Dilemma)
賽局理論 (Game Theory)
賽局理論(又稱博奕論)是一個決策思考模型,適用於有兩個或多個對手在同一個競爭#下的策略制定。而囚徒困境 (Prisoner's Dilemma) 是賽局理論中,一個最基本的靜態競爭賽局* 的思考模型。
* 靜態賽局 (Static Game Theory) 的意思是,競爭參與者皆不知道對手各自的選擇,所以是不受對方選擇影響,可以是一次性的同時行動 (one-off simultaneous actions)。
* 動態賽局 (Dynamic Game Theory) 的意思是,是相繼或連續性或互動性的重覆行動 (consequential, sequential, or interactive repeated actions)。
# 所謂「競爭」便是賽局,又或所謂「賽局」便是競爭: 競爭 = 賽局 = 博奕
賽局的意思是,一個競爭參與者的選擇,要考慮另一個競爭參與者的選擇,而作出對自己最有利的決策。假設每個競爭參與者也希望把自己利益最大化。賽局理論就是幫助競爭者計算,如何把其他競爭者的選擇納入考慮,而選擇對自己最有利的行動。
囚徒困境
情境
囚犯 A 和囚犯 B 是共同犯罪團伙,亦同時被捕。警察把 A 和 B 分開囚禁,警察分別也跟他們說以下同樣的說話:
- 「如果你招供 (confess),而對方保持緘默,你將會因為協助警方調查而獲得無罪釋放,而對方則會有 8 年有期徒刑。
- 如果你保持緘默 (silent),若對方招供,結果會是相反。你將會有 8 年有期徒刑,而對方則會獲得無罪釋放。
- 若你們兩人同時保持緘默,則你們都兩人都囚 1 年。
- 若你們兩人同時都招供,則你們都兩人都囚 5 年。」
對囚犯 A 來說,假如囚犯 B 不招供,保持緘默,我只要招供便可脫罪;但若我招供便背叛了他,他便要被重囚 8 年之多。但假若我緘默、不招供,只要囚犯 B 招供的話,我便被他背叛而被囚 8 年。如果我緘默,他也緘默,我們也被囚 1 年。如果我招供,他也招供,我們也被囚 5 年。
這盤算對囚犯 B 也一樣。
問題
囚犯 A 和 囚犯 B 各自也不知道對方的選擇,他們應該怎樣選擇呢?
答案
(1) 後果表 (consequence table)
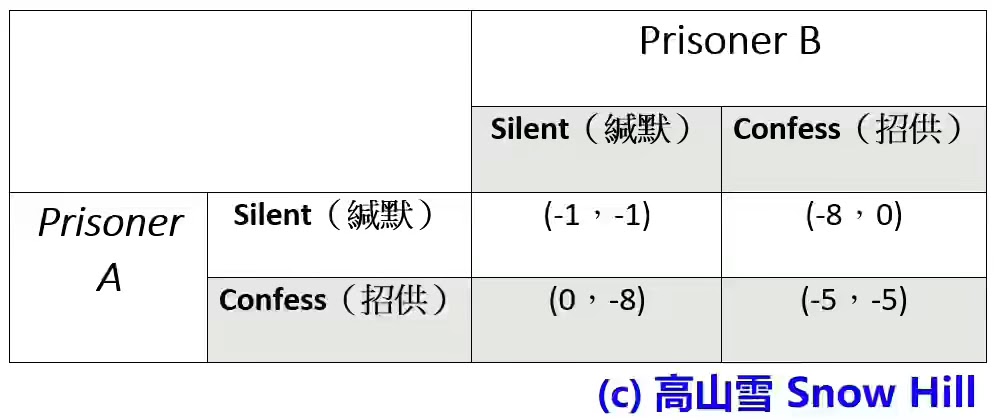
我們可以先畫一個 consequence table 來概括情況,這是一個 2 × 2 矩陣 Matrix 包括可選擇的兩個反應:招供或緘默 (see Table 1)。
在 Table 1 內,後果表示:(A 的後果,B 的後果)。
(2) 囚犯 A 角度
從囚犯 A 角度想,先想囚犯 B 的各個反應,再比較自己的各個選擇,才能看出哪個才對自己最有利。
假設:囚犯 B 選擇緘默,看 Table 2 藍色方格,垂直比較囚犯 A 的後果。對囚犯 A 來說,招供可無罪釋放,所以,招供對囚犯 A 是最有利。
假設:囚犯 B 選擇招供,看 Table 2 紅色方格,對囚犯 A 來說,還是招供對囚犯 A 是最有利。因為相比囚禁 8 年,囚禁 5 年是較輕的刑期,所以,囚犯 A 也是應該招供。
(3) 囚犯 B 角度
再從囚犯 B 角度想,看看囚犯 A 的反應,再看出哪個選擇對自己最有利。
假設:囚犯 A 選擇緘默,看 Table 3 藍色方格,橫向比較囚犯 B 的後果。對囚犯 B 來說,招供可無罪釋放,所以,招供對囚犯 B 是最有利。
假設:囚犯 A 選擇招供,看 Table 3 紅色方格,對囚犯 B 來說,招供較緘默有較輕的刑期,所以,還是招供對囚犯 B是最有利。
結果
在 2 × 2 matrix 的簡單靜態賽局中,策略是先假設對方選擇,再選擇一個對自己最有利的選擇。
- 對囚犯 A 來說,無論囚犯 B 怎樣選擇,招供對他是最有利。
- 對囚犯 B 來說,無論囚犯 A 怎樣選擇,招供也是對他最有利。
結語
在想到「只要招供便可脫罪」,理性人都會因為把自己的利益最大化而招供。這個招供的選擇便是雙方的平衡點,就是最強策略 (the dominant strategy),稱為 Nash Equilibrium。
聰明而自私的囚犯,或是理性人,總是想著如何把自己的利益最大化。明明是最理性的選擇,也是最強策略 (the dominant strategy),得到的卻不是最好的結果。這是理性人的選擇,亦即是大家也背叛大家。可是,這個所謂「理性人的背叛」選擇,帶來的卻是一個不太好的後果,就是大家都被囚 5 年,這就是困境 Dilemma 之所在。
其實如果囚犯能想想合作構成雙贏局面 (create a win-win situation),把大家的損失最少化,而非各自也只想把自己的利益最大化,效果倒是對各人最好的。在這個囚徒困境中,如果囚犯 A 和囚犯 B 都為大家著想,減輕判刑,大家都應該緘默。後果卻對大家最有利,只是被囚 1 年。當然,前提是,你要有一定信心對方不會背叛你而招供,不然你會有最壞後果,被重囚 8 年。如果你認為對方是一名理性人,那麼理性人的選擇就是你最有利的選擇。這個「信心」和「認為」就要依賴主觀機率及資訊的可信性。
這個事例道出,不是所有理性人的選擇都是最佳的選擇,不是什麼時候,也非得要把自己利益最大化不可。世界上不是所有競爭都是零和遊戲。有時候,把利益平分予其他參與者,後果可能是對你最好的。
Reference
石井俊全,統計學關鍵字典,楓葉社, Unknown year。
白波、王碩,一次讀懂博奕論,德成出版, Unknown year。
=======================
免責聲明
本網頁屬個人網誌,一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性,包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏,而導致之任何損失或損害,本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產,均受知識產權法例及權利(包括但不限於保護版權的法例)所保障。根據此法例及權利,任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下,本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
© Copyright 2021-2022 高山雪 Snow Hill. All rights reserved.













留言
發佈留言