貝氏定理 (6): 貝氏網絡 (Bayesian Network)
聯合機率 Joint Probability
如果 X 的發生是需要有 A 和 B 的出現，那就是：
P(X) = P(A, B)
如果： A = {a1, a2, a3}；B = {b1, b2, b3}
那麼：P(A, B) = {P(a1, b1), P(a1, b2), P(a1, b3), P(a2, b1), P(a2, b2), P(a2, b3), P(a3, b1), P(a3, b2), P(a3, b3)}
如果 X 的發生是需要有 A 和 B 的出現，那就是：
P(X) = P(A, B)
如果： A = {a1, a2, a3}；B = {b1, b2, b3}
那麼：P(A, B) = {P(a1, b1), P(a1, b2), P(a1, b3), P(a2, b1), P(a2, b2), P(a2, b3), P(a3, b1), P(a3, b2), P(a3, b3)}
P(A, B) 是 A 和 B 聯合機率 Joint Probability of distribution of A and B，公式是 Eq. (1)：
如果是三個變數的聯合機率 Joint Probability of distribution of A , B and C。（A, B, C）就是貝氏網絡 (Bayesian Network)，公式是 Eq. (1a)：
例子
A、B、C、D、E 的聯合機率，Joint Probability 公式是 Eq. (3)：
- P(E | C)：在 C 腦瘤出現的條件下，發生 E 頭痛的機率；
- E 的發生：E = 1； C 的條件：C = 1；⇒ 即是，P(E = 1 | C = 1)。這機率可在 Figure 2 找到，是 0.7。
- P(D | B, C)：在 B 血鈣增加或 C 腦瘤出現的條件下，發生 D 昏睡的機率；
- P(B | A)：在 A 轉移性癌症出現的條件下，發生 B 血鈣增加的機率；
- P(A)：發生轉移性癌症的機率。← 這是 Base rate。
以下 Figure 2 是一些已知的 Conditional Probabilities：
Part 1: 首先計算有昏睡及頭痛條件下，有轉移性癌症的機率：
計算 P(A=1 | D=1, E=1)：
- B = 0, C = 0
- B = 0, C = 1
- B = 1, C = 0
- B = 1, C = 1
分拆以上 Eq. (6) 內的四個機率，運用 Figure 2 提供的 Conditional probabilities 來計算：
計算 P(A=1, B=0, C=0, D=1, E=1):
計算 P(A=1, B=0, C=1, D=1, E=1):
計算 P(A=1, B=1, C=0, D=1, E=1):
計算 P(A=1, B=1, C=1, D=1, E=1):
根據 Eq. (5)，把以上的四個機率加總：
Part 2：計算有昏睡及頭痛條件下，無轉移性癌症的機率：
計算 P(A=0 | D=1, E=1)：
計算 P(A=0, B=0, C=0, D=1, E=1):
計算 P(A=0, B=0, C=1, D=1, E=1):
計算 P(A=0, B=1, C=0, D=1, E=1):
計算 P(A=0, B=0, C=0, D=1, E=1):
根據 Eq. (5)，把以上的四個機率加總：
再把 Part 1 及 Part 2 計算的 P(A=1 | D =1, E=1) 及 P(A=0 | D =1, E=1) 放回 Eq 4：
結果
在出現昏睡及頭痛狀況下，有轉移性癌症的機率有 32.4%。
總結
貝氏網絡 (Bayesian Network) 是推測、估計、反推因果關係的重要思維工具，也是人工智能 (Artificial Intelligence, AI) 及機械學習 (Machine Learning) 的基礎模型。應用層面廣泛，例如 Google Translate 翻譯中文到英文、投資預測模型、追蹤模型、決策模型。
假設：一句中文：(a1, a2, ...) 和一句翻譯的英文對應：(b1, b2, ...)。a2 的出現，多數是在 a1 之後，例如：「英」之後，多數是「國」、「文」、「語」、「美」等，而每個有意義的字組又對應英文翻譯字句。程式內蒐集了很多這類對應的中英文字句。
而將一句中文設定為隨機變項：A；一句英文設定為隨機變項：B
某機械翻譯要將一句中文翻譯成英文，便是要設定條件機率為：P(B = bi | A = ai)，要把 P(B = bi | A = ai) 算出最大的 bi 值。當中是透過貝氏統計來做。智能翻譯只是其中一項應用範疇。
我認為，重要的是學習如何運用貝氏網絡 (Bayesian Network) 的思考模型來：
- 把複雜的情況清晰化，勾畫出其中千絲萬縷的關係；
- 找出其中最關鍵、最重要的因果關係及其可能的發生機率；
- 找出其中最重要的問題、最關鍵的不確定處 (find the key problem and key uncertainty)；
- 協助我們追蹤有因果關係的事件，及悉別事件有否因果關係；
- 幫助我們作通盤考慮，及作出平衡風險利益的決策。
首先要學習繪畫 Bayesian Network（如 Figure 1），然後收集資訊（如 Figure 2 內的 conditional probabilities & base rate）。做貝氏更新來修正自己現時的預測或修正Figure 2 內的 conditional probabilities ，貝氏網絡 (Bayesian Network) 在追蹤及找出最重要的因果關係上，特別管用。
要注意，Bayesian Network 跟 Decision Tree 不同的是，後者是由決策而衍生出來的可能後果的發生機率，而前者是畫出某事件可能產生的後果，或再由某後果推上可能要有的條件。
貝氏定理的相關文章：
我的書架 | 思考的框架 (2a): 機率思考 - 貝氏思維 (Bayesian Thinking)
貝氏定理 (1): 理論 (Bayesian Theorem)
貝氏定理 (3): 貝氏因子 (Bayes Factor): 你的證據夠強嗎?
貝氏定理 (4): 貝氏規則的可能性機率 (Likelihood in Bayes Rule)
貝氏定理 (5): 貝氏更新 (Bayesian Updating)
貝氏定理 (7): 事後機率分布最大概似估計法 (Maximum a Posteriori, MAP)
貝氏定理 (8): 事前資訊質素的影響 (Prior Informativeness)
Reference
石井俊全，統計學關鍵字典，楓葉社， Unknown year。
=======================
免責聲明
本網頁屬個人網誌，一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性，包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏，而導致之任何損失或損害，本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產，均受知識產權法例及權利（包括但不限於保護版權的法例）所保障。根據此法例及權利，任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下，本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
© Copyright 2021-2022 高山雪 Snow Hill. All rights reserved.
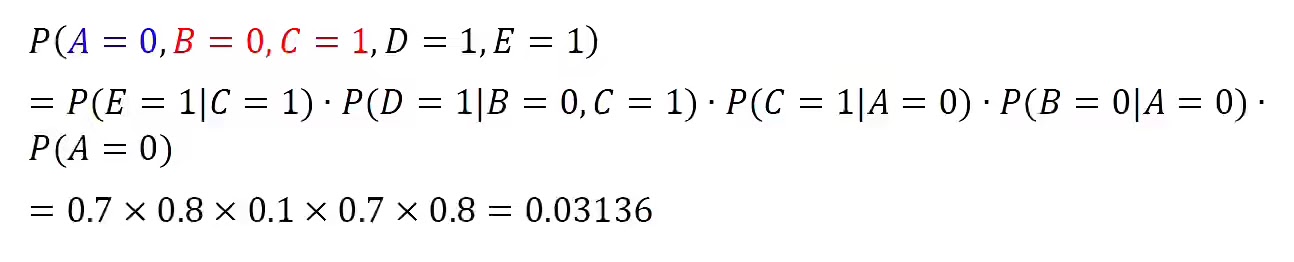
留言
發佈留言