貝氏定理 (3): 貝氏因子 (Bayes Factor): 你的證據夠強嗎?
貝氏因子 (Bayes Factor)
貝氏因子 Bayes Factor 是等同似然比率 Likelihood Ratio。這個思考模型跟之前貝氏定理的文章內描述的思考模型是不同的。
從上兩篇 <貝氏定理 (1): 理論 (Bayesian Theorem)> 文章中的 Bayes Rule 公式內 [Eq.(3)、Eq.(7)、Eq.(8)] 的變項 variables,也是用機率,條件機率來思考。但這裡的思考模型,是用 odds ratio 勝算比來思考。
貝氏因子 (Bayes Factor) 的意義是:
- 比較新信念兩者的新證據和之前舊信念的證據,兩者之間的分數。亦即是說,比起支持舊信念的證據,那新證據有多支持新信念?
在 <我的書架 | 思考的框架 (2a): 機率思考 - 貝氏思維 (Bayesian Thinking)> 文章中,我已經為 Bayes Factor 定義:
- 新信念相比舊信念,有多少可能是真的可能性 (likelihood);又或
- 新信念,相比舊信念,比較近似現實的可能性 (likelihood)。
- How many times more likely that the posterior belief is true given the new evidence as compared to prior belief?
Bayes ratio means:
the weight of evidence is in favour of the alternative hypothesis (i.e. agrees with the alternative hypothesis); or
the measure of strength of evidence in favour of the alternative hypothesis; or
to quantify the strength of evidence of alternative hypothesis over the null hypothesis; or
how many times more likely that the evidence for alternative hypothesis is true given the evidence
where:
Null Hypothesis: old belief = truth
Alternative Hypothesis: new belief = truth
Deriving Bayes Factor
從上一篇 <貝氏定理 (2): 應用例子> 的例子 2:
假設:
將 Eq. (10) 除 Eq. (12):
即:
在 Eq. (14) ,可以再拆解成:
從 <貝氏定理 (1): 理論 (Bayesian Theorem)> 文章知道 ,我們要有三個資料來計算 Posterior probability:
P(D) , P(T+ | D) , P(T+ | ¬D) 。
但從 Eq. (16) 知道,要計算貝氏因子 (Bayes Factor) ,我們只需兩個資料:
P(T+ | D) , P(T+ | ¬D) 。
又或是,從 Prior odds ratio 和 Posterior odds ratio 來計算:
貝氏因子的推論 (Inference from Bayes Factor)
Glen
(2018) 從Lee
and Wagenmakers (2014) 中總括了下面的貝氏因子的推論 (Inference
from Bayes Factor) (see Table 1) ,他們的基礎公式 Eq. (21) 跟上面筆者的 Eq. (16) 是一樣的: 
Meaning:
Likelihood of D given H1 is true: Probability of obtaining result D under the condition that the alternative hypothesis (H1) is true
Likelihood of D given Ho is true: Probability of obtaining result D under the condition that the null hypothesis (Ho) is true
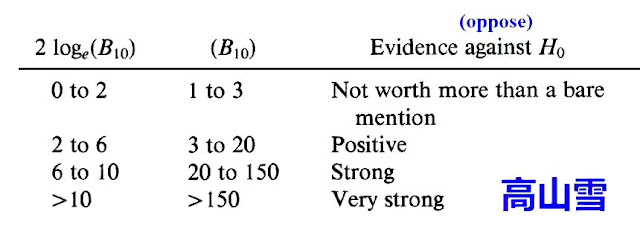
Table 1. 貝氏因子推論 (Inference from Bayes Factor) (Glen, 2018) 。
從上面 Table 1,可以得出 Bayes Factor (BF) 的以下總結:
- BF < 1:證據偏向舊信念 (Ho) 為真
- BF 在 1/3 - 1 和 1- 3:Anecdotal evidence for Ho: 軼事證據或傳聞證據。一般是來自傳聞、故事的證據。說:舊信念 (Ho) 為真,未必是真,可能只是謠傳。這些傳聞通常不具好的代表性,推論通常是不可靠的 (中文維基百科, accessed 14 Jun 2021)。
- According to Wikipedia: Anecdotal evidence is a claim relying only on personal
observation, collected in a casual or non-systematic manner, which is usually unscientific and misinterpreted by heuristics. This is a least certain type of information (Wikepedia, accessed 14 Jun 2021).
- BF = 1:證據沒有偏向
- BF > 3 或以上:數字愈大,證據愈支持新信念 (H1) 為真
- BF< 1/3 或以下:數字愈少,證據愈支持舊信念 (Ho) 為真
例子:
從上一篇 <貝氏定理 (2): 應用例子> 的例子 2,我們可以計算貝氏因子。
Given:
- 孕婦生產有唐氏綜合症嬰兒的機率是 0.15% (Prevalence) :P(D) = 0.0015
- 超聲波檢查的敏感度是 80%:P(T+ | D) = 0.8
- 超聲波檢的假陽性的機率是 8%:P(T+ | ¬D) = 0.08
問題:被超聲波檢查出陽性,而她的嬰兒確實真的患有此症的機率是多少?
In this example, Bayes ratio means:
"How many times more likely a certain condition for a test result is expected to be observed in diseased people (test positive given infected), as compared to non-diseased people (test positive given not infected)"
(Habilbzadeh & Habibzadeh, 2019).
答案:
(註:看下面其他計算方法)
=======================
註: 另一個計算 Bayes Factor for positive test 的方式:
where:
Specificity is the probability of test negative given non-diseased people, P(T- | ¬D);
Bayes Factor here is Likelihood ratio for a positive test
若果要計算 Bayes Factor for a negative test:
where:
Sensitivity is the probability of test positive given diseased patients, P(T+ | D);
Bayes Factor here is Likelihood ratio for a negative test
=======================
結果是:
即是說,這裡的「真的患病而測出陽性」證據或資訊的可信度高。
不要混淆:
這裡不是說:證據較為支持真的患病。完全不是!
這裡其實是說:證據較為支持是「證據是真或可信度高」,而不是結論!不等同於「真的患病的機率是高出10 倍」。
Bayes Factor之所以不能提供是結論。原因是,它並沒有考慮到 Prior odds:
據 Eq. (18) ,把 Prior odds ratio 乘以 Bayes Factor,就是 Posterior odds ratio:
這個 Posterior odds ratio 才是我們真正需要關心的「真的患病」的比率,這裡就是千分之15。
也就是說:
當測出陽性時,比起沒有患病(只因假陽性),真的患病的比率,是千分之15 = 1.5%。
大家只需要想想,縱使 Bayes Factor 數值是大,但 Prior odds ratio 是極少,那得出的 Posterior odds ratio 依然也很少。所以,重點在於 Prior odds ratio 有多少,才可以知道我們真正關心的 Posterior odds ratio 「真的患病」的比率是多少。
結論
Bayes Factor 是用來衡量證據本身有多真確、有多可靠的一個工具,不能提供結論 Posterior odds。
然而,Assaf and Tsionas (2018) 說道:「當沒有 Prior odds 或 Base Rate 等資料時, Prior odds 會被假定為 "1",那麼 Bayes Factor 便可以直接當成 Posterior odds」 。這是與現實生活比較接近的情況,因為在日常生活中,很多時,事情的不確定性高,同樣事件在歷史上從未發生過,這樣根本沒有 Base Rate 可供計算。在此類情況下,我們只能夠用 Bayes Factor 當成 Posterior odds。但在使用時,必須要記得這個 Prior odds 為 "1" 的假設,而且要緊密跟蹤事情的發展,不斷地更新 Posterior odds。否則,會造成極大的誤差。
相反,當 Bayes Factor 和
Prior odds 的資訊充裕,計算 Posterior odds 是沒有問題。當 Bayes Factor 和 Posterior odds 在某一次更新中已經計算出來,而因為今次的 Posterior
odds 會變成下一次更新時的
Prior odds。如果 Bayes Factor 不用每一次計算的情況下(如:此例子),那麼,
在下一次更新時,我們便可以使用先前的 Bayes
Factor 和 Prior odds(即上次的Posterior
odds) 輕易快速計算今次的 Posterior
odds 了。而不久,會變成 constant。除非有新的資訊出現,否則不用更新。
特別要留意:Bayes Factor 是否在 1/3 - 1 和 1- 3 的兩個區間? 因為這代表:Anecdotal evidence for Ho ,即:軼事證據或傳聞證據:是不可靠的。當這些證據或資訊出現,要小心處理,因為其可信度低,可以不用更新模型。尤其,要避免自己在這些資訊下的認知偏誤。
貝氏定理的相關文章講述:
我的書架 | 思考的框架 (2a): 機率思考 - 貝氏思維 (Bayesian Thinking)
貝氏定理 (1): 理論 (Bayesian Theorem)
貝氏定理 (4): 貝氏規則的可能性機率 (Likelihood in Bayes Rule)
貝氏定理 (5): 貝氏更新 (Bayesian Updating)
貝氏定理 (6): 貝氏網絡 (Bayesian Network)
貝氏定理 (7): 事後機率分布最大概似估計法 (Maximum a Posteriori Estimation, MAP)
貝氏定理 (8): 事前資訊質素的影響 (Prior Informativeness)
References
Stephanie Glen (2018), Bayes Factor: Simple Definition, StatisticsHowTo.com: Elementary Statistics, available from: https://www.statisticshowto.com/bayes-factor-definition/.
Michael D. Lee and Eric-Jan Wagenmakers (2014), Bayesian Cognitive Modeling: A Practical Course, Cambridge University Press.
Robert E. Kass and Adrian E. Raftery (1995), Bayes Factors, Journal of American Statistical Association, 90 (430), 773-792.
Farrokh Habilbzadeh and Parham Habibzadeh (2019), The Likelihood Ratio and its Graphical Representation, Biochem Med (Zagreb), 29 (2), 1-6. https://doi.org/10.11613/BM.2019.020101
Albert Assaf and Mike Tsionas (2018), The Bayes Factor vs. P-Value, Tourism Management, 67, 17-31.
Wikepedia, Anecdotal Evidence, https://en.wikipedia.org/wiki/Anecdotal_evidence, accessed 14 Jun 2021.
中文維基百科,軼事證據, https://zh.wikipedia.org/wiki/%E8%BB%BC%E4%BA%8B%E8%AD%89%E6%93%9A, accessed 14 Jun 2021.
=======================
免責聲明
本網頁屬個人網誌,一切言論純屬個人意見及經驗分享。本人無法保證在本網誌所提供的資料有關內容的真確性和完整性,包括但不限於任何錯誤、誤差、遺漏、或侵權性質、誹謗性質或虛假性質的信息或任何其他可導致冒犯或在其他方面引致發生任何追索或投訴的資料或遺漏,而導致之任何損失或損害,本人概不承擔任何有關法律責任。
版權聲明
本網誌的所有資料、圖像與相片、文本屬本人所有專屬財產,均受知識產權法例及權利(包括但不限於保護版權的法例)所保障。根據此法例及權利,任何未經授權使用的資料均屬侵權行為。在未經本人明確同意授權下,本網誌資料、圖像與相片、文本之全部或部份均不可被使用、複印、改編、修改、發表、儲存或以其他方式複製分發、發佈或向公眾提供、銷售、傳送該等版權作品作任何用途。
© Copyright 2021 高山雪 Snow Hill. All rights reserved.


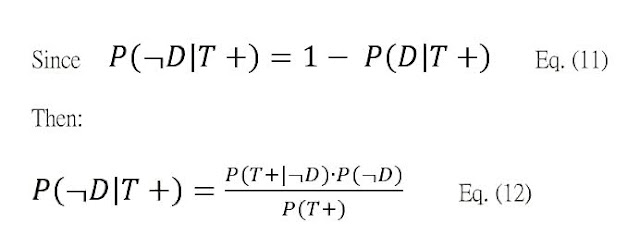








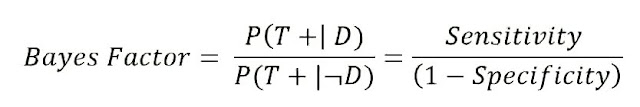













留言
發佈留言